I consider that aesthetics and the sense of wonder occupy a vital place in the teaching of the sciences and mathematics, and that without these ourlearning has no ‘soul’ and no creative expression.

There is a great deal of lament these days about the poor teaching of the sciences and mathematics, and with good reason. Its effect at the national level is all too visible; we have become a nation that specializes in doing well at examinations, but fails to carry the momentum beyond that point. The learning of technical skills (with, pragmatically, the first place being given to the skill of answering examination questions) has come to occupy a central place in our curricula. This pattern stretches far and wide, and the well known coaching centres for the various entrance examinations in this country are among the worst offenders.

The ‘cure’ for this, if there is any, has to start at the school level. The teaching of the sciences and mathematics must leave behind a sense of wonder and reverence for the great beauty and intricacy of the world — the world of the very small and the world of the very large; but this feeling must not be limited to the physical form of the world. Here is what Henri Poincaré wrote about the scientific endeavour:

The scientist does not study nature because it is useful; he studies it because he delights in it, and he delights in it because it is beautiful. If nature were not beautiful, it would not be worth knowing, and if nature were not worth knowing, life would not be worth living. Of course I do not here speak of that beauty that strikes the senses, the beauty of qualities and appearances; not that I undervalue such beauty, far from it, but it has nothing to do with science; I mean that profounder beauty which comes from the harmonious order of the parts, and which a pure intelligence can grasp.

It is because simplicity and vastness are both beautiful that we seek by preference simple facts and vast facts; that we take delight, now in following the giant courses of the stars, now in scrutinizing [through] the microscope that prodigious smallness which is also a vastness, and now in seeking in geological ages the traces of a past that attracts us because ofits remoteness.

What are we to do with Poincaré’s words? Surely it is possible to engage students in a way that heightens the appreciation of the ‘harmonious order of the parts’ of the world, and that engenders a delight in ‘simple facts and vast facts’? Surely it is possible to teach in a way that science and mathematicsbecome poetry?

When a child is young, it is absurdly easy to bring about the sense of wonder; one only has to bring the child into contact with nature, with the enormity of life and the universe; and nature herself will teach the child inthe best way possible. Rachel Carson said this very poignantly:

I sincerely believe that for the child…it is not half so important to know as to feel. If facts are the seeds that later produce knowledge and wisdom, then the emotions and the impressions of the senses are the fertile soil in which the seeds must grow. The years of early childhood are the time to prepare the soil. Once the emotions have been aroused — a sense of the beautiful, the excitement of the new and the unknown, a feeling of sympathy, pity, admiration or love — then…knowledge about the subject…has lasting meaning. The winds, the sea, and the moving tides are what they are. If there is wonder and beauty and majesty in them, science will discover these qualities. If they are not there, science cannot create them. If there is poetry in my book about the sea, it is not because I deliberately put it there, but because no one could write truthfully about the sea and leave out the poetry …

But as the child’s intellectual abilities mature, the teacher has to strive a bit further, for now a new kind of beauty comes within reach of the mind — that of the principles that seem to govern the development of nature and the wide world, and which science and mathematics seek to find and describe in the simplest terms possible. These principles are part of the poetry, and there is great joy in coming upon them.

What is it about principles that appeals to us so much? It is important for the teacher to ask this question, and to determine what leaves behind the deepest impression on a growing mind, particularly at the middle school and high school levels. In my own teaching I have found the following to be ofgreat significance:

• Appreciation of the beauty and economy of good description
• Appreciation of predictive power, and of the power of unifying principles
• The pleasure of finding unexpected connections
• The pleasure of seeing the simplicity that results from good translation.

Examples from science

Here are some examples from the world of science, of principles and unifying themes that carry great predictive power. As one studies them, onemarvels at the power of principles!

1. The principle of levers: so absurdly simple a principle, so easy to state, and yet it allows us to grasp the mechanisms of such a varied set of household devices! — from crowbars, to kitchen tongs, pliers, can openers, nail cutters, scissors, bicycle hand brakes, …
2. The kinetic theory of gases, and the model of heat and gas pressure that it creates in our minds: heat is understood as the energy of movement of the gas or liquid molecules, and pressure as the effect of the incessant bombardment by molecules. Using the model one quickly sees why the gas laws simply have to be true — at least qualitatively; e.g., why, when we increase the temperature of a fixed amount of gas, while keeping its volume fixed, the pressure also increases. And one sees the possibility of heating a substance by making its molecules ‘dance’ using microwaves, as in a microwave oven.
3. Bernoulli’s principle (The total energy in a steady flowing fluid system is constant along the flow path. With an increase in speed comes a decrease in pressure) — a non-obvious principle that helps us make sense of such varied phenomena as the lift of airplane wings, the functioning of a perfume spray bottle, the laterally curving trajectory of a football when it is suitably kicked (this is the ‘banana kick’ of David Beckham fame), and the phenomenon of swing bowling in cricket.
4. Conservation laws — of energy, momentum, and angular momentum; the scope of phenomena that they allow us to understand is truly vast, stretching from simple daily life phenomena to stellar evolution, to how NASA sent its Voyager spacecraft on a journey to the stars with some help from Jupiter, and to the strange discovery that the Earth day was shorter during earlier eras, and the moon closer to the Earth than now.¹
5. The periodic table, and the intricate patterns it reveals in the properties of the different elements. There is the stirring story of Mendeleev’s prediction of the existence of Gallium, which he had named eka-aluminium (“first after aluminium”). Apparently when it was discovered by a French chemist, its reported density differed from the value Mendeleev had predicted. This provoked him to ask for a fresh measurement of the density, and when this was done, the value coincided with his predicted value!

There are so many more such themes which can be listed, and each opens up a whole new world: Darwin’s theory of natural selection; Mendel’s laws of heredity; the mechanism of DNA replication, and how it explains heredity; the phenomenon of mitochondrial DNA, and how it allows us to uncover the pathways of human evolution; Bohr’s model of the atom, and the understanding it provides of spectra associated with various atoms, and the notion of quanta; Le Chatelier’s principle, and the way it enables us to predictthe effects of changing the conditions of a chemical reaction.

There is a quote of Richard Feynman’s which belongs here: ‘The world looks so different after learning science. For example, trees are made of air, primarily. When they are burned, they go back to air, and in the flaming heat is released the flaming heat of the sun which was bound in to convert the air into tree, and in the ash is the small remnant of the part which did not come from air, that came from the solid earth, instead…These are beautiful things, and the content of science is wonderfully full of them. They are very inspiring, and they can be used to inspire others.’

But, having said all this, it is wise to end on a cautionary note. The pleasure and happy abandon we feel when, armed with just a few principles, we are able to make sense of the world must not make us lose touch with the essential mystery of the world. It is one of the traps we human beings fall into — that of substituting words for the actual and then feeling that we have grasped the real thing. Feynman was fond of narrating a conversation which his father had with him: ‘See that bird? It’s a brown-throated thrush, but in Germany it’s called a halzenflugel, and in Chinese they call it a chung ling, and even if you know all those names for it, you still know nothing about the bird. You only know something about people — what they call that bird. We could easily trap little children with this human tendency. Ask a child, “What makes things fall down? ”, and you get the textbook answer, “Gravity makes things fall down.” Push a little further and ask, “What is gravity”; then youget, “Gravity is the thing that makes things fall down.” ’ Well.

Substituting real phenomena with words a bit too early in one’s schooling can kill questioning. It would be a wonderful experiment if we can get children to try explaining phenomena without using catch-all words like ‘gravity’ and‘energy’ and ‘evolution’. Who knows, it could be the beginning of a realscientific adventure!

Examples from mathematics, the ‘science of patterns’

Mathematics is rich in elegance, simplicity and interconnectedness. It is difficult to give illustrative examples, if only because there are so many of them! The examples we give seek to show beauty and interconnectedness rather than the power of any overarching or unifying theory.

1. Euclidean geometry has been studied for well over two millennia; Euclid’s great text, The Elements, which lays down the structure of the subject through precisely stated axioms, postulates and ‘common notions’, is not only an extraordinary model of presentation but also of axiomatic development. That it continues to serve as a model for mathematical writing more than twenty centuries after its publication is a testimony to how great a work it is.² Here is a comment on the book:

Euclid’s ‘The Elements’ form one of the most beautiful works of science in the history of humankind. This beauty lies more in the logical development of geometry rather than in geometry itself. It is not the diagrams that excite our interest; rather it is the way the concepts interconnect…The ‘Elements’ are elegant. Elegance in mathematics is characterized by simplicity and clarity. An elegant presentation is easy for the reader to follow. But elegance is not only in the presentation, it is in the selection of definitions and proofs. The elegant definition is the one that makes the rest of the theory easy. The elegant proof is the one that is easiest to follow, one that is designed just right to fit the goal.

[David Joyce, Clark University]

One of the gems in Euclid’s ‘The Elements’ concerns prime numbers. Prime numbers have long been a subject of intense curiosity, for they are easy to define and yet contain a vast number of secrets. A question that readily arises is: How many of them are there? The answer is that they are limitless in number, and Euclid’s proof of this is “by contradiction”. The proof is a masterpiece of economy; it achieves its purpose without getting trapped by the question, What is the next prime after a given one? Hardy remarks that the proof remains …as fresh and significant as when it was discovered — two thousand years have not written a wrinkle on [it]; he adds: The proof is by reductio ad absurdum, and reductio ad absurdum, which Euclid loved so much, is one of a mathematician’s finest weapons. It is a far finer gambit than any chess gambit: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.

Here is a fact that brings home the mystery of the primes. Recently it was found that 2 ^32582657-1, a number with nearly ten million decimal digits, is prime. But Euclid assures us that beyond this monster, there lie infinitely more primes …

Sadly, the trend today is that many mathematics teachers in India and elsewhere have never read Euclid (or any of its equivalents); so it is not surprising that geometry is now one of the most poorly taught portions of the curriculum. One of the pedagogically most convenient ways of introducing a formalized style of logical reasoning, and of the notion ofelegance in mathematics, has been cast by the wayside.

2. Pythagoras’s theorem has been known since very ancient times, and in cultures widely separated in time and space. It has the distinction of having been proved in a larger number of ways and by a more varied class of people than any other proposition. One such is a ‘proof without words’ attributed to the twelfth century Indian mathematician Bhaskaracharya (author of Lalavati); another one is from James Garfield, a former president³ of the USA!⁴

We are given a right-angled triangle with legs a, b, and hypotenuse c; we must show that a²+b²=c². Note that the area of the triangle is ½ (base x height)= ½ ab.

Garfield’s proof may be illustrated using these figures:

Using the formula for area of a trapezoid (half the product of the height and the sum of its parallel sides), we find that its area is½(a+b) (a+b). But the area is also equal to ½ ab+ ½ab+ ½c², as it is made up of two copies of the original triangle and half of a c x c square. Equating these two expressions, we get c²= a²+b², as desired. (Bhãskarã’s proof is similar to this, but it uses four copies of the given triangle.)

3. A primitive Pythagorean triple (“PPT” for short) is a triple of coprime positive integers such that the sum of the squares of the first two is equal to the square of the third one; for example, (3, 4, 5) and (5, 12, 13). PPTs are related to Pythagoras theorem in an obvious way. Interest in such triples goes back to further than 1600 B.C., as can be seen from the Plimpton clay tablets excavated in ancient Babylon.

The way PPTs are generated is a nice illustration of the theme of interconnectedness. If we divide the first two numbers of the triple by the third number, we get a pair of rational numbers which yield a rational point on the unit circle (one whose coordinates are rational numbers). Conversely, each rational point on the unit circle yields a PPT. So, finding PPTs is equivalent to finding rational points on the unit circle. One such point is Q (*1, 0). Now consider a line * through Q, with a rational slope t. It will intersect the unit circle again at a rational point whose coordinates can be found by solving a pair of equations. By giving arbitrary rational values to t we get an unlimited number of rational points on the unit circle, and from them an unlimited number of PPTs. Example: t=²⁄₅; yields the point (²¹⁄₁₉, ²⁰⁄₂₉), and the PPT (21, 20, 29). This solution ‘attaches’ to each PPT a rational point on the unit circle, by an invisible thread as it were.

What is ‘elegant’ about this solution? Observe how we transformed the problem from one about integers to one about a line and circle, using coordinates; we mapped the problem into a domain which we know much better (coordinate geometry), and so were able to use resultsfound earlier.

This analysis illustrates an important aspect of mathematics — its compressibility. Here is mathematician Bill Thurston: ‘Mathematics is amazingly compressible: you may struggle a long time, step by step, to work through some process or idea from several approaches. But once you really understand it and have the mental perspective to see it as a whole, there is often a tremendous mental compression. You can file it away, recall it quickly and completely when you need it, and use it as just one step in some other mental process. The insight that goes with this compression is one of the real joys of mathematics.’⁵

4. Another nice instance of interconnectedness is seen when we study ordered partitions. Pick a positive integer n, and list all the ways in which it can be written as a sum of positive integers, with the understanding that the order in which we list the summands is to be taken into account; so 1+2 is listed separately from 2+1. Also, a ‘sum’ of just one integer is acceptable. The different expressions so obtained are then the ‘ordered partitions’ of n. So the ordered partitions of 2 are: 2, 1+1; we write these for convenience as 2, 11 (read this as “one one” and not “eleven”). The ordered partitions of 3 are: 3, 21, 12, 11; the ordered partitions of 4 are: 4, 31, 13, 22, 21, 121, 112, 11. And for 1 there is just oneordered partition, namely, 1 itself.

If we list the number of ordered partitions corresponding to each number, we stumble upon something very pleasing indeed:

We see a wonderful pattern taking birth here: 1, 2, 4, 8, …; surely the next number ‘ought’ to be 16? And so it is; the ordered partitions of 5 are 16 in number: 5, 41, 14, 32, 23, 31, 131, 113, 221, 212, 12, 21, 121, 1121, 112, 11. What a pleasing discovery!

What has happened here is a typical mathematical experience — the discovery of an unexpected pattern. It is certainly one of the great joys of studying the subject. But the analysis must not stop here; now we must explain why such a pattern manifests, when there is nothing in the statement of the problem that would suggest it. If we are able to do so, what a supreme moment it would be! — to understand the hidden geometry of a problem, as it were, and to uncover its links with other problems.

5. Transformations in geometry are a strongly unifying theme, powerful and elegant at the same time. They connect a modern theme in mathematics, that of function, with an ancient one, Euclidean geometry. Concepts from abstract algebra are easy to see in action when we studytransformations.

Euclidean geometry for long was regarded as absolute, perhaps because of the way it connects with daily life, and it was only in the middle of the nineteenth century that its liberation came; then it spread its wings and manifested in diverse forms. It was Felix Klein, a German mathematician, who first put forward a unifying way of viewing these different geometries, using the notion of transformations. This change of perspective had an enormous influence on the development of the subject. A nice example of a theorem that is elegantly handled using transformations is Napoleon’s theorem (supposedly discovered by Napoleon, but more likely by one of his generals; he was fond of taking along mathematicians on his campaigns). Given a triangle ABC, we construct equilateral triangles BPC, CQA, ARB on its three sides, all lying outside the given triangle. If we now draw the segments AP, BQ, CR, we find that they have the same length and pass through a common point — the Fermat point of the triangle. This has many attractive properties; for example, if A, B, C are villages, and we wish to put up a rural dispensary that can be accessed by all three villages, then the best location to use is the Fermat point. Moreover, the six angles created at this point are equal to one another.

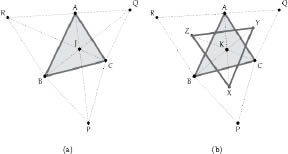
Next, we locate X, Y, Z, the centres of BPC, CQA, ARB, and draw the segments AX, BY, CZ; we find that these three lines too meet at a point (marked K). This is the Napoleon point of the triangle. Even better: we find that XYZ is equilateral, and this remains so regardless of the shape of ABC.

As earlier, we can continue quoting examples indefinitely; but we have to bring this section to a close. A key question is whether these examples can be adapted to constructivist pedagogy; but this is readily done.

Closing remarks

There is poetry in science, and there is poetry in mathematics. And every child should have a taste of it. Only a small fraction of the children who study these subjects in school will study these subjects later in life, but it is surely every child’s right to experience — if only for a day, or a lesson — their power and beauty, which lie within every person’s reach. I think that as teachers we owe this to our students.

In the past it has seemed to some that by delving into the mysteries of nature and explaining them in terms of simpler phenomena, we spoil the poetry of God’s creation. Keats reflected this feeling when he wrote:

There was an awful rainbow once in heaven:
We know her woof, her texture;
she is given In the dull catalogue of common things.
Philosophy will clip an angel’s wings.

Why would Keats have had such a response to science? Could it have been because of the rise of technology and the fever of industrialization in England during his day, and the terrible working conditions of the common people? Or because of a know-it-all attitude on the part of post-Newtonian era intellectuals whom he had met? Or because he had seen how when we place a beautiful phenomenon in the ‘dull catalogue of common things’ we tend to lose our child-like sense of wonder and our reverence for life? It is hard to say; such spill-over attitudes are common, and they say more about our mental makeup than about what we do. And to lose this sense is to not live at all.

What about the feeling that to ‘unweave’ a rainbow is to destroy it? Surely, the truth is not so weak that it will diminish in stature when one explains it? ‘To live at all is miracle enough.’⁶ And if along the way one also gets a glimpse of the intricate workings of nature and exults in its incredible beauty, it is only a bonus we have been granted.⁷ So, when with Keats we ‘Behold upon the night’s starred face / Huge cloudy symbols of a high romance’, why not see this as an invitation to enter into a romance that will enrich us so greatly? On this journey we will also delve into the rich historical tradition of science, with its many stirring stories.

Richard Dawkins writes about his book Unweaving the Rainbow:

The title comes from Keats, who was talking about Newton unweaving the rainbow and thereby spoiling the poetry, which I think is nonsense. When you do explain something, you usually uncover still greater mysteries, which are even more beautiful. The unweaving of the rainbow eventually led to spectroscopy, and spectroscopy is how we know what the stars are made of, by detecting what chemical substances are in the stars. Looking at red shift in the far distant parts of the universe shows us that the universe is expanding; that shows us when the universe began, it shows how big the universe is. A great deal of what we now know about the universe has come to us from unweaving the rainbow.

But there is another aspect to what Keats wrote, and it would be foolish to pass over it. In today’s science there are also questions of ethics involved — much more so than in earlier eras. Are there boundaries beyond which one must not tread? Are there experiments one must not do? Though such questions may not appear to form part of the scientific endeavour, it is important that students think about these matters, though answers may prove elusive to find; and this should be done as part of the learning of science, not separately. In the hands of a thoughtful teacher, such questions can integrate in a natural way with those of mainstream science and leave in its wake an appreciation of the potentially overpowering complexity of human life and civilization. But this is an area that needs to be dwelt on at length, separately.

I shall let the last word be that of John Muir, my favourite naturalist author:

This grand show is eternal. It is always sunrise somewhere; the dew is never all dried at once; a shower is forever falling; vapour is ever rising. Eternal sunrise, eternal sunset, eternal dawn and gloaming, on sea and continents and islands, each in its turn, as the round earth rolls.

Notes

¹ This happens because of tidal friction and the resulting slow but steady loss of energy. The person who first predicted this effect was George Darwin, son of Charles Darwin. It means that the dinosaurs would have had a twenty-two hour day; so they would have had to hurry through their tasks a bit faster than we do! They would also have seen the moon at closer quarters than we do.

² The Elements is second only to the Bible in the number of editions published (over a thousand).

³ He was a senator when he found the proof, and went on to become President later inhis career.

⁴ One longs for a time when presidents and prime ministers of powerful countries would exhibit some interest in geometry. Imagine a session at a UN summit meeting being devoted to an exchange of experiences with problems of geometry rather than problems of terrorism; how peaceful such a world would be!

⁵ Quoted by the Mathematics Focus Group for the National Curriculum Framework2005.

⁶ Mervyn Peake, poet.

⁷ Whether we deserve this bonus is not very clear.